What unique properties of quantum mechanics give quantum computers their power? How do we scale up the physics that governs atoms to the size of a mainframe? Our theory team is led by Professor Stephen Bartlett, Professor Andrew Doherty, and Dr Arne Grimsmo. Our research interests range from understanding the fundamental differences between classical and quantum information processing to designing the best quantum architectures for tomorrow’s supercomputers.
Research Projects
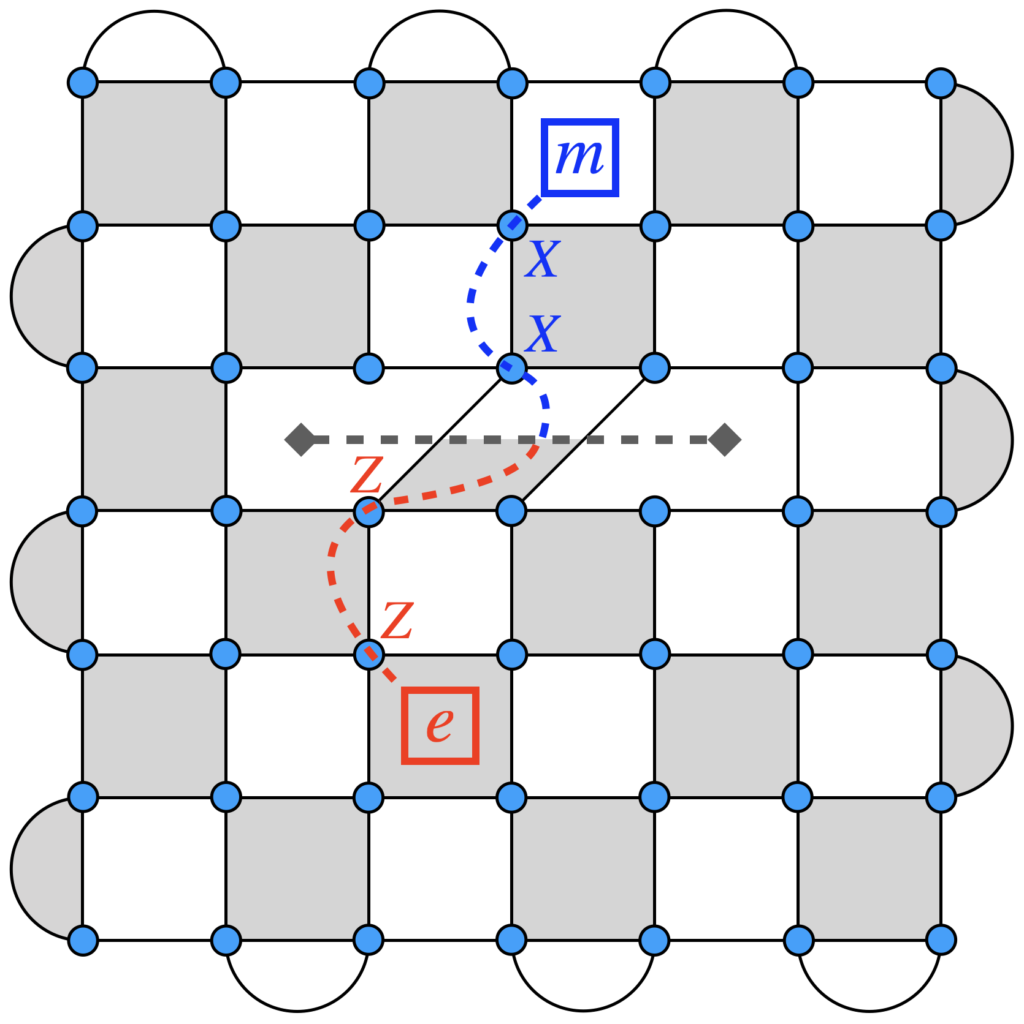
Quantum error-correcting codes
Dr. Seok-Hyung Lee, Dr. Dominic Williamson
Quantum systems are extremely sensitive to their environment. When we encode quantum information into a system, this information is rapidly corrupted due to environmental noise. Suppressing these errors — and correcting them faster than they can occur — is critical for building full-scale, useful quantum computers. This is only possible with quantum error-correcting codes, making them central to the design of quantum computers. Quantum codes have deep connections to the physics of oscillators, topological phases of matter, and even the holographic principle from string theory.
Quantum characterisation, verification and validation
Dr Robin Harper, Dr. Salini Karuvade
Quantum computers are intrinsically prone to noise. While there’s a growing interest in exploring the capabilities of noisy intermediate-scale quantum devices, the ultimate goal is to achieve fault-tolerant quantum computing. However, this transition poses significant challenges that call for efficient methods of error characterisation on large-scale systems. As part of this challenge we look at how to leverage the fundamental quantum properties of the devices to extract crucial information about the noise in those devices.
Physical implementations of quantum computers
Dr. Abhijeet Alase, Dr. Giacomo Panteloni, Dr. Thomas Smith
How do we engineer the fundamental physics of atoms, electrons, or photons to process quantum information? There are numerous platforms that are being developed for quantum computation. At the University of Sydney alone, we have groups pursuing qubits based on electrons trapped in semiconductor quantum dots, ions trapped in electromagnetic fields, microwave plasma oscillations of superconducting electric circuits, and rare-earth ions implanted into crystalline hosts. Despite a wide range of competing approaches, no clear “winner” has yet emerged. In this program, we theoretically investigate a wide variety of quantum computing architectures, and develop novel methods of encoding and manipulating quantum information.
Many-body quantum optics
Dr. Alexander Johnston, Dr. Sahand Mahmoodian
These are systems where photons interact with one another through a nonlinear medium — usually atoms or artificial atoms. These systems are difficult to model and understand for a number of reasons: they are quantum systems whose Hilbert space grows exponentially with the number of particles and they are open systems that are often driven by external sources of light, e.g., lasers. We use a number of different theoretical techniques to model these systems including: scattering matrix techniques, which can give analytic insight into the behaviour of these systems, as well as numerical techniques such as Matrix-Product State methods.
Foundations of quantum mechanics
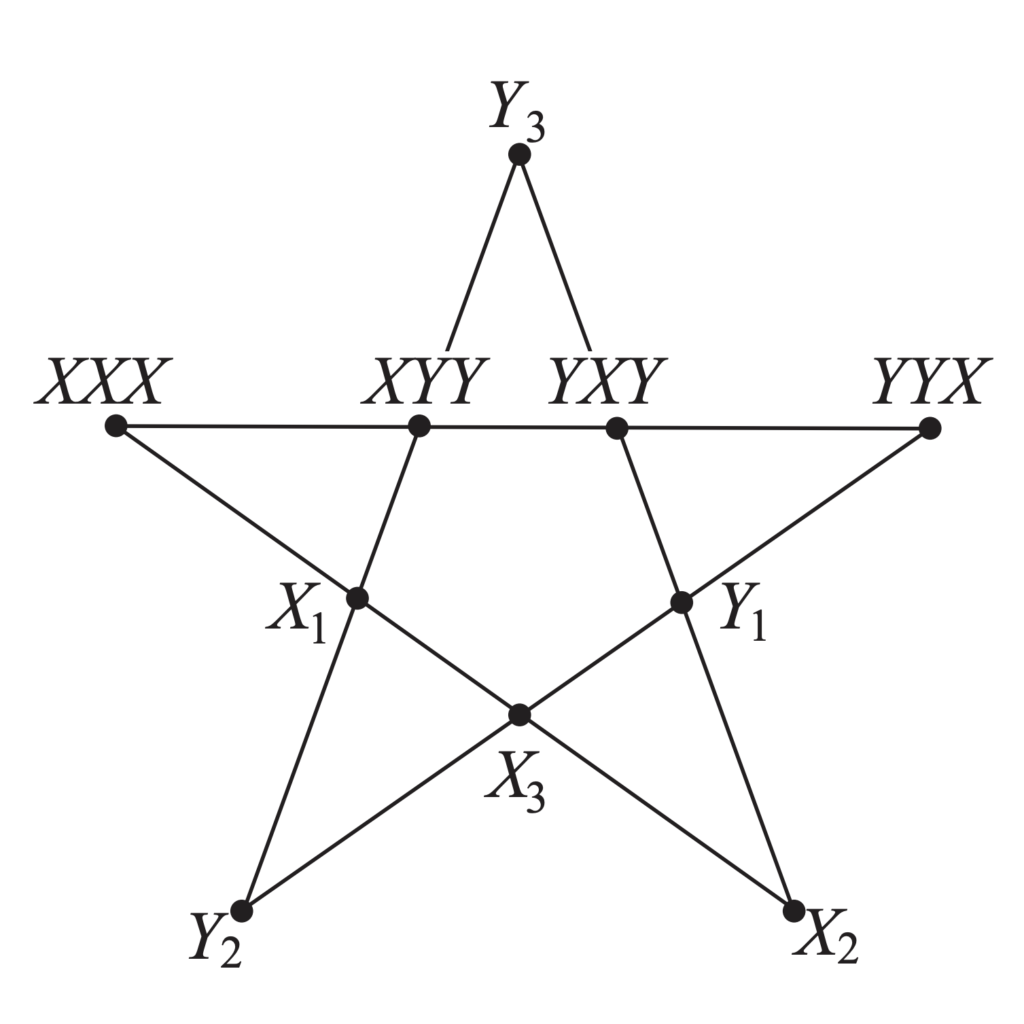
While it is believed that a quantum computer will have abilities beyond any classical computer, we currently only have a handful of problems for which we believe that a quantum computer would be useful. One way to obtain more insight into the class of problems for which a quantum computer might have an advantage over its classical counterpart is by studying the fundamental difference between quantum and classical information processing. Questioning what makes a quantum system non-classical is not only a deep question about the physical world but also a less ad hoc way of discovering quantum advantage.
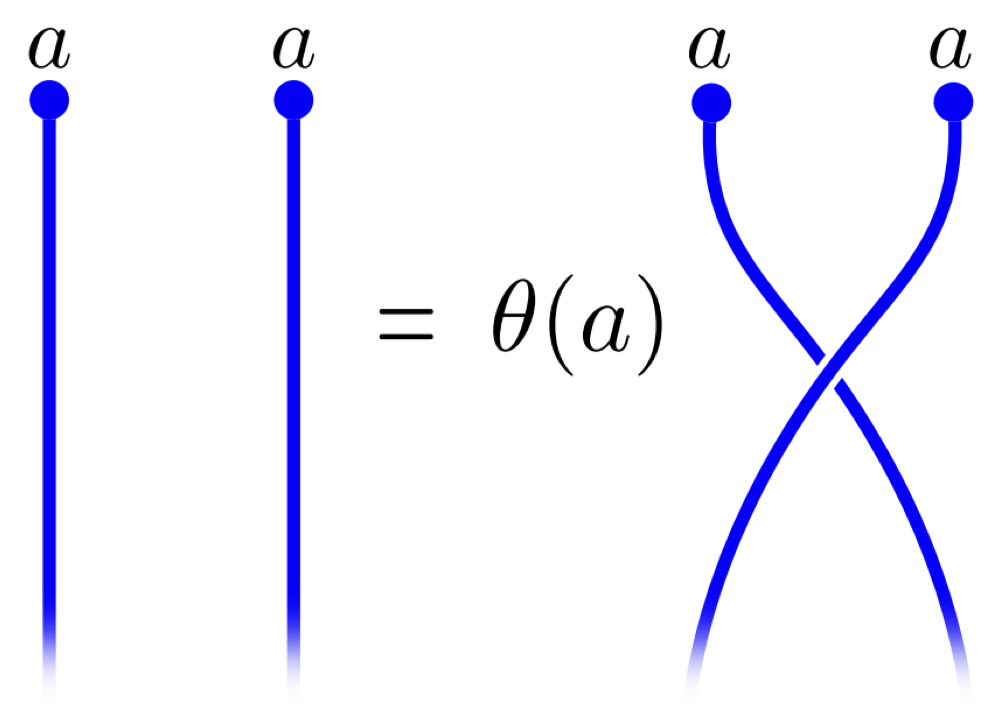
Topological phases of matter
Dr. Abhijeet Alase, Dr. Dominic Williamson
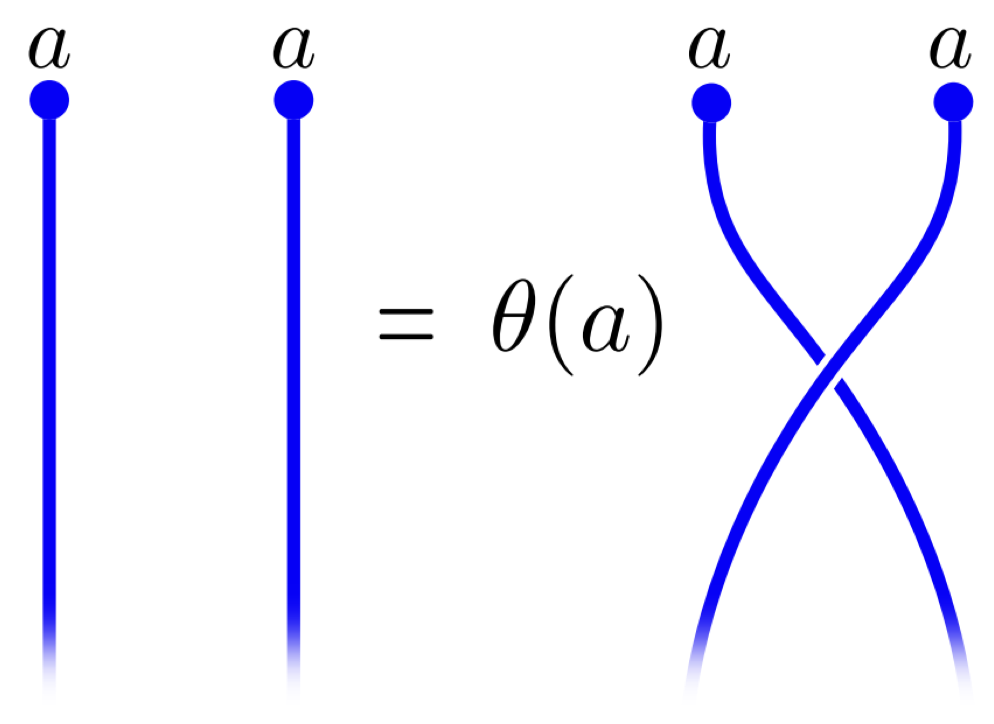
Quantum entanglement gives rise to new phases of matter beyond the classical theory of symmetry breaking and local order parameters. These phases are characterised by nonlocal topological properties that are governed by topological quantum field theory. This leads to striking new phenomena such as the splitting of an electron into anyonic quasiparticles that carry fractional charge. These phases of matter can be used as quantum error-correcting codes due to their natural robustness to local perturbations.